Глава 2.1-3. Переходные процессы регулирования производительности магистральных газопроводов и их влияние на функциональную надежность газоснабжения

Во второй главе докторской диссертации Жидковой М.А. «МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ТРУБОПРОВОДНОГО ТРАНСПОРТА ГАЗА ПРИ ОПТИМАЛЬНОМ ПРОЕКТИРОВАНИИ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ» выполнены теоретические исследования динамических свойств основных технологических объектов газопроводов - линейных участков (ЛУ) и автоматизированных компрессорных станций (КС). Рассчитан эффект перерегулирования производительности компрессорных станций, являющийся источником снижения функциональной надежности магистральных газопроводов. Установлена его взаимосвязь с характеристиками линейных участков, компрессорных станций и параметрами настройки регулирующих устройств. Исследованы переходные процессы при плавном и дискретном регулировании производительности КС, приведена оценка их влияния на функциональную надежность газоснабжения

М.А.Жидкова впервые показала как порождаются трансцендентные аналитичекие функции при математическом моделировании нестационарных динамических процессов в системе линейных участков магистрального газопровода с компрессорными станциями

Как выглядят трансцендентные аналитические функции в 3D-пространстве? Увидеть удалось благодаря появившемуся в 1985 году мощному графическому расширению «ГРАФОР» для языка программирования ФОРТРАН (Баяковский Ю.М., Галактионов В.А., Михайлова Т.Н. ГРАФОР. Графическое расширение фортрана. М.: Наука, 1985)

Осмысление этого изображения (на рисунке) привело к получению очень интересных математических результатов у В.Н.Царенко (сотрудник группы М.А.Жидковой). Появление возможностей визуализации трансцендентных аналитических функций привели в конечном итоге к дальнейшему развитию положений теории моделирования переходных процессов в магистральных газопроводах М.А.Жидковой

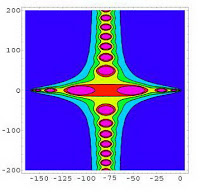
На рисунке приводится изображение 2D-проекции трансцендентной аналитической функции по данным из монографии М.А.Жидковой (1979,стр 63)

Именно этот рисунок иллюстрирует замечательные свойства симметрии в расположении собственных значений (нулей) трансцендентных функций в поле комплексных чисел при математическом моделировании нестационарных процессов в линейном участке газопровода. Цветные рисунки иллюстрируют потрясающие возможности системы Mathematica по графической визуализации трансцендентных аналитических функций в поле комплексных чисел. Эти функции возникают при решении разнообразных прикладных задач описывающихся системами уравнений с частными производными

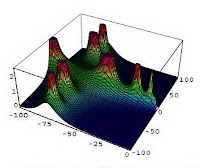
А этот рисунок иллюстрирует рельеф (3D-изображение) поверхности той же трансцендентной функции в поле комплексных чисел

До появления в 1988 году системы Mathematica визуализация трансцедентных аналитических функций, впрочем, как и любых других нетривиальных математических объектов, являлось необычайно сложной задачей. Эти объкты, в основном, «находились» в голове математика. И от того, как четко он себе их представлял, порой зависел успех или забвение предлагаемых им методов или теорий

С появлением таких систем как Mathematica считавшаяся уделом для «избранных» профессия математика стала увлекательным и просто интересным занятием. Сегодня в системе Mathematica пишутся статьи и книги, проводятся научные исследования и создаются изумительные по своей красоте абстрактные графические образы. И, порой, даже сложно себе представить, что без нее можно было бы обходиться
_____________________________________________________________________________________________________________
Структура второй главы диссертаци М.А.Жидковой:
_____________________________________________________________________________________________________________
2.1. Линейные решения уравнений газовой динамики при изотермическом движении газа (62)

2.2. Анализ переходных процессов в участке трубопровода на основе нелинейных уравнений газовой динамики (80)

2.3. Аналитические решения дифференциальных уравнений при квазинеизтермическом течении газа (98)

2.4. Компрессорная станция магистрального газопровода как объект регулирования (102)

2.5. Переходные процессы при дискретном регулировании производительности компрессорной станции (109)

2.6. Переходные процессы при плавном регулировании производительности компрессорной станции (121)

2.7. Оптимальное регулирование производительности магистральных газопроводов (129)

Выводы и рекомендации по второй главе (140)
_____________________________________________________________________________________________________________
Далее приводятся страницы (61 - 141) пятой главы
_____________________________________________________________________________________________________________
_____________________________________________________________________________________________________________
Ваши комментарии перед публикацией я просматриваю. Поэтому я оставляю за собой право публиковать или нет комментарии с подписью Анонимный